Let’s say we want to estimate $\pi$ with Monte Carlo. We get some pairs of random numbers $(x, y)$ with both $x$ and $y$ uniformly distributed between 0 and 1. Approximately $\frac{\pi}{4}$ of those should fall within the unit circle, so we can get an estimate of $\pi$ by multiplying proportion of points that fall within that circle by 4.

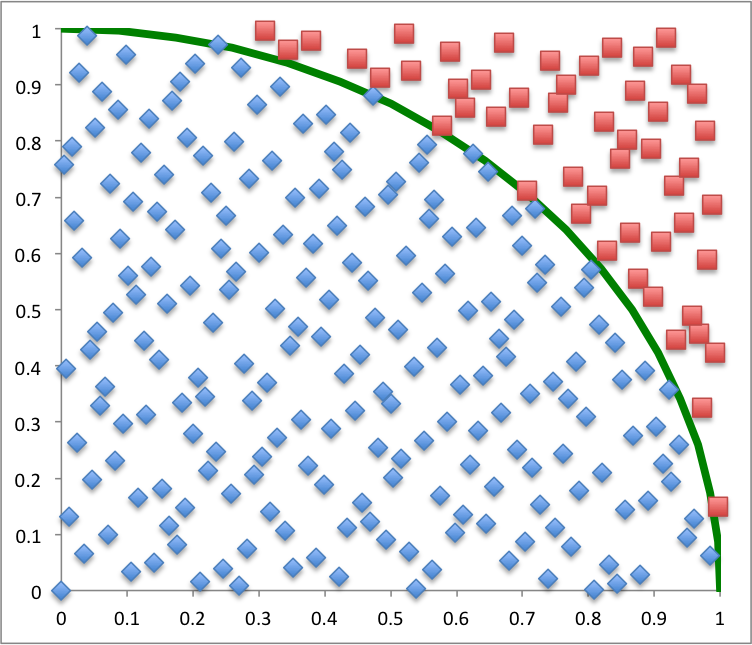
Knowing that some implementations of pseudorandom number generators are better than others, we decide to take a look at the first 256 points. Can you tell which of the two pictures below shows uniformly distributed random numbers?

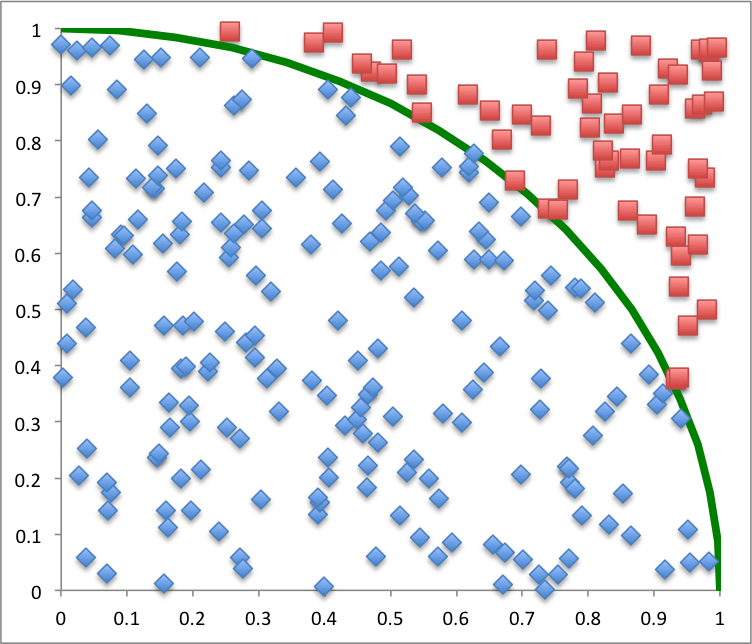
The first picture is from std::default_random_engine and std::uniform_real_distribution in GCC. The points tend to form clumps and leave some empty spaces. This is normal, the distribution is uniform only in the limit.

The second picture is Halton sequence. The points there are distributed more evenly, with no clumps and no large empty areas. They are not independent, though. Such sequences are called quasi-random or subrandom. Sobol sequence is used more often, but in this example we’ll stick with Halton because it’s simpler.

Let’s get more points:

#include <iostream>
#include <random>

double halton(unsigned index, unsigned base)
{
  double f = 1, r = 0;
  while (index) {
    f /= base;
    r += f * (index % base);
    index /= base;
  }
  return r;
}

int main(void)
{
  std::default_random_engine gen;
  std::uniform_real_distribution<double> dist;
  unsigned pseudo_count = 0, quasi_count = 0, next = 1;
  std::cout << "N\tPseudo\tQuasi\n";
  for (unsigned i = 1; i <= (1 << 21); i++) {

    // Pseudo-random
    double x = dist(gen), y = dist(gen);
    if (x * x + y * y < 1) {
      pseudo_count++;
    }

    // Quasi-random (Halton)
    double a = halton(i, 2), b = halton(i, 3);
    if (a * a + b * b < 1) {
      quasi_count++;
    }

    // Results
    if (i == next) {
      std::cout << i 
                << "\t" << 4. * pseudo_count / i
                << "\t" << 4. * quasi_count  / i << "\n";
      next <<= 1;
    }
  }
}

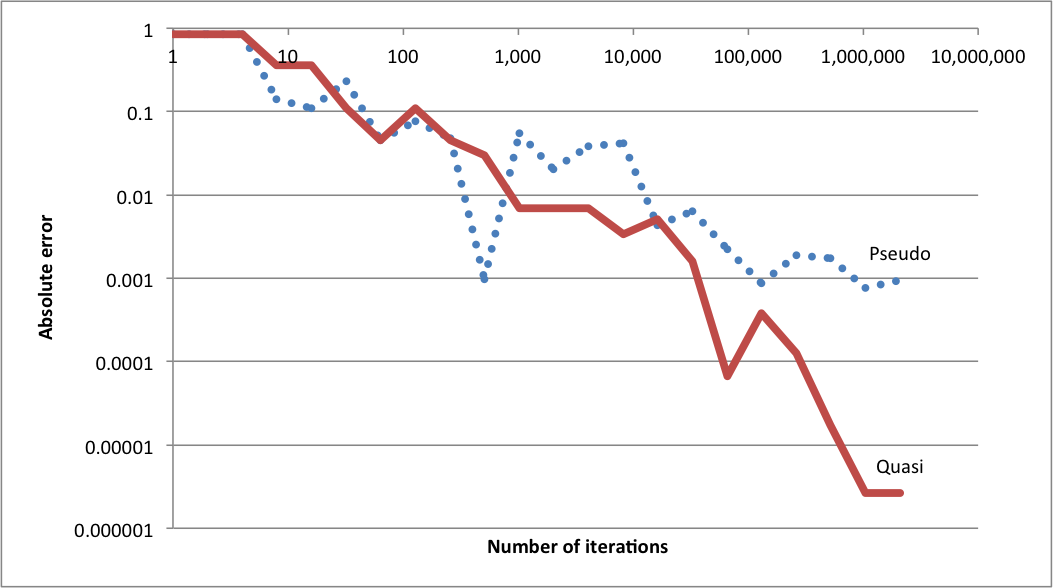
In this case it’s clear that quasi-random sequence works better: