What is greater, $e^{\pi}$ or $\pi^e$?

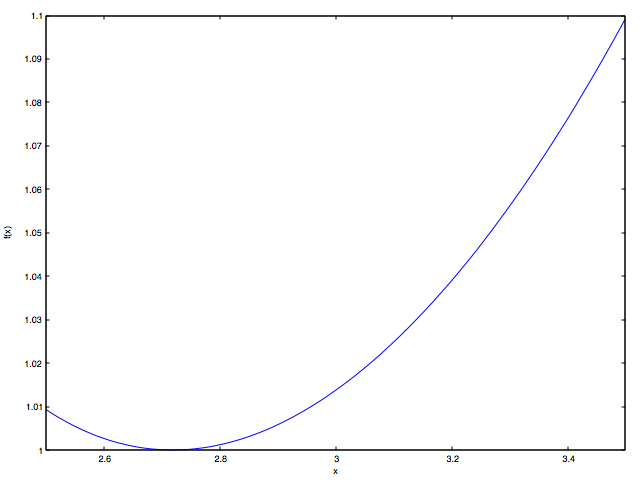
Consider a function $f(x)=\frac{e^x}{x^e}$ and check if it’s greater than 1 at $x=\pi$.

It’s easy to see that $f(e)=1$, but we want to know which way the function goes from there.

$f'(x)=e^x x^{-e} - e^x e x^{-e-1}=(x-e) e^x x^{-e-1}$ which is positive for all $x>e$. So this function goes up when $x>e$. We know that $\pi>e$, therefore $f(\pi)>1$ and $e^{\pi}>{\pi}^{e}$.

wxMaxima plot:

plot2d(%e^x/x^%e,[x,2.5,3.5],[ylabel,"f(x)"]);